小学6年生の算数の時にきちんと習っているはずなんだけど。
統計自体は非常に興味あるものである。
このengadget日本版の調査ではなく、MMD研究所が作成した調査を元に書いた記事のようだ。
なお、MMD研究所の調査データサマリにおいては、格安SIMについてMVNOという表記が全くなされていないことを先に記しておく。
調査データをMMD研究所のほうでも見てみる。
現在支払っているスマートフォンの平均月額料金は6,823円、大手3キャリアユーザーは平均7,433円、格安SIMユーザーは平均2,067円
出だしが異なる。
MMD研究所は、15歳以上のスマートフォン(大手3キャリアユーザー N=973、格安SIMユーザー N=106、その他 N=26)を所有する男女1,105人を対象に「2016年スマートフォンの利用料金に関する調査」を実施致しました。※大手3キャリア:docomo、au、SoftBankを指します。
大手3キャリアのユーザの母数は973、格安SIMユーザの母数は106である。これで、平均月額料金は6,823円とされている。
現在支払っているスマートフォンの平均月額料金は6,823円、大手3キャリアユーザーは平均7,433円、格安SIMユーザーは平均2,067円
ワイモバイルはどっちなんだろうな。MVNOのように格安って言えるほどには安くないと思うけど。UQコミュニケーションズはMVNOのUQ mobileとルータ契約だけのWiMAXに分かれているから迷わないだろうけど。
調査データ記事には元の回答月額料金が記載されていない。そのため、この「現在支払っているスマートフォンの平均月額料金」がどう算出されたのかは類推するしかないが、どうやら回答された月額金額を相加平均(いわゆるみんなが知ってる算術平均)したものに見える。3キャリア平均と格安SIM平均のそれぞれの母数を掛け、加算して平均を取ると6,905円になるので、まあそんな感じだろう。
7,433×973=7,232,309
2,067×106=219,102
(7,232,309+219,102)÷(973+106)=6,905
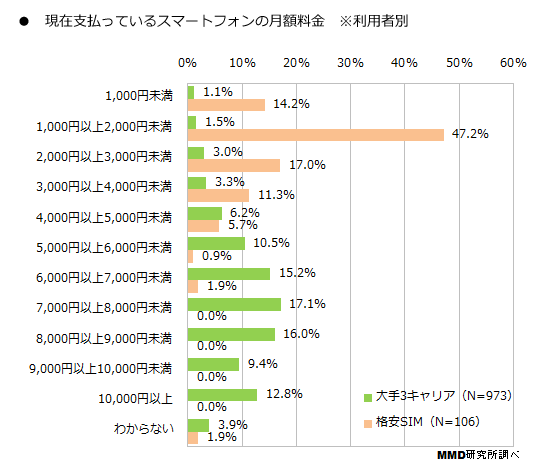
しかし、分布を自ら書いているのを見ても分かるように、母数が全く異なる数字を全部足し込んで平均を出しても、その平均には意味が無い。 分布が記載された「現在支払っているスマートフォンの月額料金」グラフを引用する。
分布が全く異なる。格安SIMのほうは1,000円以上2,000円未満が47.2%で大きな山となっている。しかし、グラフ内にも記載されているように母数が異なる。9倍も異なる母数の数字を単純に足し込んで相加平均を取ったのでは、全く意味の無い数字になる。せめて母数を合わせるべきだろう。いや、この相加平均が世の中の実相を表している可能性もゼロではない。もう少し調査データサマリを見てみよう。
もともとの全体の母数である1,105人は有効回答数である。
【 調査結果サマリー(※一部抜粋)】
■ 現在支払っているスマートフォンの平均月額料金は6,823円、
大手3キャリアユーザーは平均7,433円、格安SIMユーザーは平均2,067円■ スマートフォンの適正だと思う月額料金は平均4,066円、
大手3キャリアユーザーは平均4,371円、格安SIMユーザーは平均1,723円■ 現在利用しているスマートフォンの端末代金、平均金額は52,369円
■ スマートフォン端末に支払ってもよいと思う平均金額は26,450円
・ 調査期間:2016年2月19日~2月23日
・ 有効回答:1,105人
以上である。つまり、この調査では大手3キャリアが格安SIMの9倍という回答数であることについては、特に検証されていない。実態でも9倍の差があるのか、それ以上なのかそれ以下なのか。
調査時期は半年前だが、総務省の調査では9倍以上である。
(1) 移動系通信(携帯電話・PHS・BWA)
携帯電話の契約数は1億5,149万(前期比+1.0%、前年同期比+5.4%)、移動系通信(携帯電話、PHS及びBWA。以下同じ。)の契約数は1億5,816万(前期比+0.6%、前年同期比+4.6%:単純合算では1億7,864万)となっています。
(中略)
(2) MVNO
MVNOサービスの契約数※は997万(前期比+4.7%、前年同期比+25.9%)、移動系通信の契約数に占める比率は6.3%(前期比+0.2ポイント、前年同期比+1.1ポイント)となっています。
約16倍弱である。MMD研究所の調査結果とは大きく乖離している。やはり、意味の無い平均だった。
ここまで書いてきて、意味の無い平均以外にも大きな問題があることに気付いた。
「現在支払っているスマートフォンの月額料金」ってなんだよw。何について聞いているんだ?言葉通りスマートフォンの分割代金なのか、スマートフォンで使用している回線の料金なのか、その総和なのか。ポンコツですわ、この調査結果。異なるものをまとめて聞いている。
多分スマートフォン関係で毎月払っている総和だと思うけど、それだとオレみたいに端末一括で月額を抑えた奴は安いことになるし、端末代金を分割にしていればその代金が毎月乗ってくるから高い。端末代金を一括で払ったiPhoneの料金はこんな感じ。12月は手数料など色々あったので高いが、定常運転になった1月2月は2,000円台。ここだけ見ればMVNO並。

でもまあ、毎月払っている額については認識できても、明細まで覚えている奴はあまりいないよな。調査する側がきちんと切り分けて設問を作らないと、何を聞いたのか分からない調査結果が出るという例である。
話を戻す。平均の話だった。
それぞれのグループ(格安SIM,大手3キャリア)内で平均を出すのはまあいいだろう。最頻値にして欲しいけど。どうしても平均を出すなら、単純な相加平均だけじゃなく、他の平均を使うべき。Excelにも複数の平均系関数が用意されている。関数を使えば難しい数式を考える必要はない。
相乗平均
調和平均
一般化平均
COVARIANCE.P 関数 - Office のサポート
COVARIANCE.S 関数 - Office のサポート
前にも書いたけど平均は小学5年生で履修するけど、統計的に考察するのは小学6年生。
文部科学省の新学習指導要領・生きる力「第2章 各教科 第3節 算数:文部科学省」では下記のように定められている。下線と太字はオレが入れた。「新学習指導要領・生きる力」ということでわざわざ「生きる力」と入れているわけで、生きていく上で大切だと思うんだが。
〔第5学年〕
1 目標
(1) 整数の性質についての理解を深める。また,小数の乗法及び除法や分数の加法及び減法の意味についての理解を深め,それらの計算の仕方を考え,用いることができるようにする。
(2) 三角形や平行四辺形などの面積及び直方体などの体積を求めることができるようにする。また,測定値の平均及び異種の二つの量の割合について理解できるようにする。
(3) 平面図形についての理解を深めるとともに,角柱などの立体図形について理解できるようにする。
(4) 数量の関係を考察するとともに,百分率や円グラフなどを用いて資料の特徴を調べることができるようにする。
(中略)
B 量と測定
(1) 図形の面積を計算によって求めることができるようにする。
ア 三角形,平行四辺形,ひし形及び台形の面積の求め方を考えること。
(2) 体積について単位と測定の意味を理解し,体積を計算によって求めることができるようにする。
ア 体積の単位(立方センチメートル(cm3),立方メートル(m3))について知ること。
イ 立方体及び直方体の体積の求め方を考えること。
(3) 量の大きさの測定値について理解できるようにする。
ア 測定値の平均について知ること。
(4) 異種の二つの量の割合としてとらえられる数量について,その比べ方や表し方を理解できるようにする。
ア 単位量当たりの大きさについて知ること。
第5学年だけじゃなく第6学年にも。
〔第6学年〕
1 目標
(1) 分数の乗法及び除法の意味についての理解を深め,それらの計算の仕方を考え,用いることができるようにする。
(2) 円の面積及び角柱などの体積を求めることができるようにするとともに,速さについて理解し,求めることができるようにする。
(3) 縮図や拡大図,対称な図形について理解し,図形についての理解を深める。
(4) 比や比例について理解し,数量の関係の考察に関数の考えを用いることができるようにするとともに,文字を用いて式に表すことができるようにする。また,資料の散らばりを調べ統計的に考察することができるようにする。
(中略)
D 数量関係
(1) 比について理解できるようにする。
(2) 伴って変わる二つの数量の関係を考察することができるようにする。
ア 比例の関係について理解すること。また,式,表,グラフを用いてその特徴を調べること。
イ 比例の関係を用いて,問題を解決すること。
ウ 反比例の関係について知ること。
(3) 数量の関係を表す式についての理解を深め,式を用いることができるようにする。
ア 数量を表す言葉や四角,三角などの代わりに,a,xなどの文字を用いて式に表したり,文字に数を当てはめて調べたりすること。
(4) 資料の平均や散らばりを調べ,統計的に考察したり表現したりすることができるようにする。
ア 資料の平均について知ること。
イ 度数分布を表す表やグラフについて知ること。
(5) 具体的な事柄について,起こり得る場合を順序よく整理して調べることができるようにする。
これを見てもわかるように、学習指導要領では5年生は平均の出し方を学ぶだけだが、6年生では分散や分布についても学び統計的に考察するということになっている。つまり、すぐに平均出してドヤ顔しているやつらは5年生レベルで留まっていて、6年生レベルには達していないということになる。いわゆるゆとり教育の時代の学習指導要領はわからないが、現在6年生でやるレベルの話を義務教育内にやらないというほどには難しい内容でもないので、中学卒業までにはやったものと思う。
オレの記憶でも平均は5年生、統計的な見方・考え方は6年生だったような気がするので、多くの人は算数のレベルで習っているものと考えられる。なんでも平均を出す人間の蔓延はまさに教育の敗北。
ほかにも突っ込みどころがあるんだけど長くなったのでここまで。
![Microsoft Office Home and Business 2016 [ダウンロード][Windows版](PC2台/1ライセンス) Microsoft Office Home and Business 2016 [ダウンロード][Windows版](PC2台/1ライセンス)](https://images-fe.ssl-images-amazon.com/images/I/41e3SVzLXUL._SL160_.jpg)
Microsoft Office Home and Business 2016 [ダウンロード][Windows版](PC2台/1ライセンス)
- 出版社/メーカー: マイクロソフト
- 発売日: 2015/09/30
- メディア: Software Download
- この商品を含むブログを見る

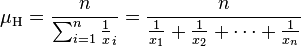

![【購入者特典付き(2016/03/31まで延長)】Microsoft Office 365 Solo(1年版) [オンラインコード] [ダウンロード][Win/Mac/iPad対応](PC2台/1ライセンス)【国内正規品】 【購入者特典付き(2016/03/31まで延長)】Microsoft Office 365 Solo(1年版) [オンラインコード] [ダウンロード][Win/Mac/iPad対応](PC2台/1ライセンス)【国内正規品】](https://images-fe.ssl-images-amazon.com/images/I/51drNO3tFKL._SL160_.jpg)